Figure 3.1)
Read this section if:
You want to verify for yourself the validity of the Path Analysis main assertions and understand the details of how and why Path Analysis works.
Skip this section if:
You will accept the main assertions and are just interested in using Path Analysis to make conclusions about what suspensions can do and comparisons between various bikes.
This section is moderately difficult.
As stated above:
Path Analysis works because the mass of the rider/main triangle dominates all mass in a bicycle. In addition, the differences in mass movement of the suspension members between different designs with similar component paths are relatively small. This makes the ground and the rider/main triangle the only two significant masses in bicycle physics.
Furthermore, all forces on the rear suspension members, other then those directly between suspension members (through pivots and so forth), are directed through the PA specified components. Since suspension member mass is not significant and the suspension members control motion between the two significant masses, it is enough to consider the forces between the PA specified components.
We now look at this a little more closely.
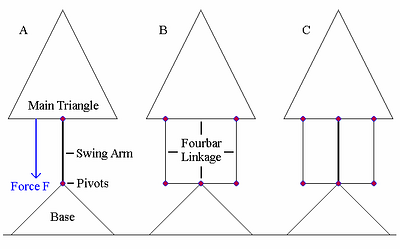
Consider Figure 3.1 A). Here, we have a main triangle and swing arm attached to a base by a pivot. This is actually the proper model with which to analyze bicycle suspensions, minus some contributions from the front fork. If the force F were calibrated to the force of gravity, you would have most of the situation for the analogous dual suspension bike, in a particular gear (no human rider could really produce such high values, but the values can be reduced by tilting the mechanism backward, into the page). Note that the main triangle can move only in a certain restricted way relative to the base and that the lower pivot, analogous to the rear axle on a bike can move only in a certain path relative to the main triangle.
{We have drawn the pictures vertically symmetrical and the linkages to form parallelograms. But the model should be taken more generally to include any typically shaped front triangle and lengths of linkage members. The model should also be considered in all reasonable positions.}

Figure 3.1)
Next, consider Figure 3.1 B). Here, we have a main triangle and a 4-bar linkage attached to a base by a pivot. This produces precisely the same paths as the mechanism in Figure 3.1 A). In fact, if we neglect the masses of the swing arm and linkage, we would have identical situations in both A) and B). Figure 3.1 C) shows both suspensions on the mechanism at once, from which we see that both suspensions will work harmoniously with one another. This foretells an analytical device that I have conceived, called a natural mirror bike, which we will discuss below in “The Natural Mirror Bike.” section. Now the question is, “Can we neglect the masses of the suspension members?”
If the mass of the swing arm were very large compared to the mass of the main triangle and the mass of the 4-bar linkage were very small compared to the main triangle, then it is easy to see that PA would not apply. In A), the main triangle would rotate around the upper pivot with relatively little motion from the swing arm when F is applied. In B), the main triangle and linkage would move very differently from A), the linkage moving more drastically then the swing arm, producing a very different physical situation. But this is not the case in a bicycle.
A typical dual suspension frame weighs about five to six pounds, without the rear shock. Of this, the rear might take up 2.5 pounds. Now in bikes for which there is any utility in comparison, the mass difference between any two types of rear suspensions is going to be less then half a pound. The rider/main triangle, on the other hand, averages about 150 pounds, at least. This leads to a mass difference of less then 0.3 % between the vast majority of mechanisms.
In addition, the movement of mass through suspension compression depends largely on the relative motion of the specified components, within the range of motion for all viable suspension bikes. Considering the movements of the links in a 4-bar linkage, one sees that the overall movement of mass is very similar to the movement of mass in a mono-pivot swing arm (though not exactly the same). The movement of mass in the GT i-Drive is almost identical to a mono-pivot, the only (insignificant) differences being the movement of the eccentric on the swing arm and of the “dogbone”.
As a result, we may neglect the suspension members and focus exclusively on the paths that they produce, as we have drawn in Figure 3.2 A) for the mechanisms in Figure 3.1). Here, we have drawn a circular path for the lower pivot about the main triangle. This contains all of the significant information concerning how the mechanisms will work. Figure 3.2 B) shows the type of motion allowed by all equivalent mechanisms.
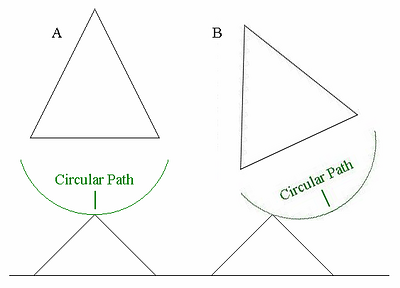
Figure 3.2)
We have demonstrated these principles for a 4-bar vs. a mono-pivot, but they apply in general, since the masses of suspension members will always weigh about the same as the examples here.