iii) PA thus passes this third test, while ICT shows its fourth flaw: again, arbitrary nature.

Now note that the Ellsworth Truth and Dare are as close to wp-coaxial 4-bars as is practical without the rear pivot interfering with the cogs.  In these two bikes, then, the configurations of the upper links will be of little consequence, beyond suspension rate.  Their rear wheel axle paths will be very close to those of mono-pivots, even more so then the bikes plotted in the “Typical Horst Link Designs” section.  Path Analysis tells us that they will thus have performance under pedaling and bump feedback that is almost identical to mono-pivots, with main pivots in the same places as those of the respective Ellsworth bikes (minus suspension rate of course).

It is rather ironic that ICT is arbitrary in a situation oh so close to the bikes that Ellsworth produces.

Tony Ellsworth disputes this, saying, “You say the Truth ict has a path very close to a single pivot.  TI doesn't.  Don't think I haven't drawn each.  And if it is ‘similar' your assuming that the amount of difference is not feel able or insignificant.  Again, you are dead wrong.”

It is true that each person must decide what is significant or “similar”, and what is not, but it is obvious that the variation between the axle path of the Truth and the most similar mono-pivot is many orders of magnitude less then the radius of curvature.  The reader may draw his or her own conclusions.

This third Ellsworth failure is due to the same deficiencies exposed in test number 2, as well as, almost certainly, the use of a dynamic model for determining squat and anti-squat that is just wrong.

It is impossible to more directly analyze the problems with Ellsworth's dynamic model for determining IC location along the chain line, since they do not give a quantitative account in the patents.

We have been given third party accounts of the dynamics behind ICT that are said to come directly from Ellsworth.  This dynamic model is extremely simple.  We know that this third party has had extensive contact with Ellsworth and some of his explanations included what were said to be Ellsworth quotes, from e-mail correspondence.  In addition, some of the problems in the ICT qualitative theory of squat verses anti-squat correspond well with problems in the third party's dynamics, suggesting that the third party accounts do represent Ellsworth's theory.  However, although there is some indication that the third party accounts do represent Ellsworth's theory and the dynamic model in the accounts is extremely simple to analyze, we feel an analysis is not appropriate without some further corroboration.

If we come into possession of Ellsworth's dynamic model, with some additional confidence that we have a correct and complete account, we will further analyze the problems with it at that time.

Nevertheless, we can get a further idea that the Ellsworth dynamics are problematic by conducting the following exercise:

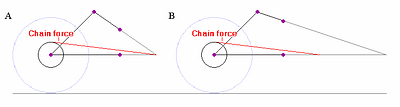
Begin by considering the wp-coaxial 4-bars in Figures 5.5 A and B), which are identical, aside from the upper, forward pivot location, giving a different IC location.  As is always the case with wp-coaxial 4-bars, the two configurations would perform identically (suspension rate aside).

Figure 5.5)
Click to enlarge

Now, suppose on both of the above suspensions, we imagine: increasing the rear wheel radius; correspondingly decreasing the rear cog radius; and keeping everything else the same.  This produces the configurations in Figures 5.6 A and B).  ICT does not ascribe any significance to the location of the rear axle, so supposedly nothing has changed in either case.

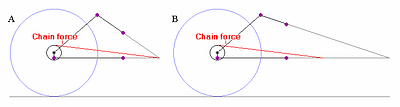
Figure 5.6)
Click to enlarge

If ICT were correct that location of the rear axle does not matter, then the suspensions in Figures 5.6 A and B) must also be identical.  But, as is shown, only one of them could have a chain through the IC, for a given front chain ring and BB location.  ICT thus claims that they are different.  So we see yet another problem in that ICT is again in conflict with itself.

But there is no limit to the possible configurations we can create with this exercise.  We have thus shown that ICT is incorrect in all non-limiting cases.

All of this indicates that, whatever dynamics Ellsworth is using to determine IC location along the chain line, it is really screwy.

Everything that we have done here requires Nature Varies Smoothly, in order to examine the limiting cases and, in the last demonstration, to use them as a reference for examining the non-limiting cases.

Numerous ICT (and PCL) adherents have formed psychological blocks to accepting the fact that Nature Varies Smoothly, in clinging to their theories.  This appears to effectively include Ellsworth and Kojima, who utterly rejected the limiting case analyses at the time of the discussions and, we are told, continue to not accept the validity of examining limiting cases.

In our original ICT analysis, we explained:

{An aside:  One may ask, “Do our parallel and pp-coaxial 4-bars fall under the ICT prescription?”  Put mathematically, our two 4-bars are limit points in the space of ICT 4-bar bikes.  ICT 4-bars come infinitesimally close to our two 4-bars, therefore, our two 4-bars impact on ICT theory to the same extent as any ICT 4-bar, regardless of whether or not one wants to define them as such.  Looking at the parallel 4-bar in a practical way; the upper and lower links cannot be exactly parallel in any real world bike, so any such bike will in fact have an IC very far away (about half in the forward direction).  Trying to establish a parallel chain line will put the chain line through this IC as accurately as any chain line can be through any IC on any bike.  For the pp-coaxial” 4-bar, the coaxial pivot is indeed a true IC.}

To this, Mike Kojima replied:

BBBWWWAAAHHH!!

It is rather shocking that someone, said to have an engineering degree, would not understand these very elementary mathematical and physical concepts.

In any case, ICT now seems to recognize mass, but clearly mass is still not handled properly, as fundamental problems remain.

The above demonstrations, any one of which is fatal, expose Ellsworth failures in understanding the physics of bicycle rear suspensions.

But there is yet another problem with ICT, involving claims for improved braking.

Ellsworth's recipe for a 4-bar suspension, to supposedly achieve their claims for performance under braking, is explained below in quotes from U.S. patent 6,471,230.  Figure 5.7) shows “FIG. 2”, etc. of U.S. patent 6,471,230, which is the diagram for the explanations to follow.

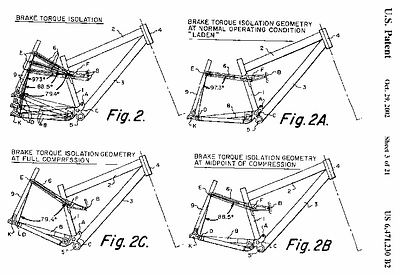
Figure 5.7)
Click to enlarge

Ellsworth explains the linkage configuration, leading to the claims of increased braking performance, as follows:

...reducing brake torque reactivity of the suspension system by positioning a brake about the rear wheel of the bicycle so that braking forces created by the brake acting on the rear wheel are nearly perpendicular to a straight line passing through the rearward pivot points of the upper and lower rocker arms, thereby reducing brake torque reactivity of the suspension system.