iv) Test number 1:

As noted above, ICT identifies two types of forces: the chain force, and the acceleration forces of squat and anti-squat.  How Ellsworth treats the chain force is the heart and soul of ICT.  So let us examine whether or not Ellsworth has a proper understanding of this critical issue.

If we eliminate the acceleration forces, this will allow us to focus attention on the chain force.  To do this, one can imagine a bike sitting on ice; when the rider pedals, the bike will not accelerate, so squat and anti-squat will be eliminated.  Putting a bike in a trainer that clamps the rear wheel axle will similarly eliminate the acceleration forces.

One can also imagine eliminating the effect on the rider/main triangle from the unsuspended fork lowers and the front wheel, which Ellsworth does not directly address anyway.  This can easily be done by suspending the fork uppers from the ground.

With acceleration removed, consider the following:

PA correctly tells us that the parallel and pp-coaxial 4-bars will behave identically, if the path tangents are identical.

In the case of the “parallel” 4-bar, ICT tells us that we should have a chain line parallel to the swing arm, since the IC is moving around at infinity.  ICT and the “parallel/mono” natural mirror thus give us a “parallel” chain theory for non-accelerating mono-pivots.

In the case of the “pp-coaxial” 4-bar, ICT tells us that we should have a chain line through the coaxial pivots.  As a result, ICT and the “pp-coaxial/mono” mirror give us a “Pivot At the Chain Line” theory for non-accelerating mono-pivots.

ICT theory thus gives conflicting prescriptions for the same physical situation.

Furthermore, in the “PCL Problems – Some Further Calculations” section, we directly calculate the proper pivot location, for a non-accelerating mono-pivot, using full-blown classical dynamics.  We find there that the chain should neither be parallel nor at the pivot.  The same will be true for our two 4-bars.

ICT's fundamental prescription of a chain through the IC thus gives erroneous results, even when taken in isolation from other forces Ellsworth considers.

PA thus passes this test, while ICT shows its first two flaws: inconsistency and incorrectness, having a fundamentally flawed central assertion.

Since ICT is inconsistent and incorrect, in the absence of acceleration and forces coming through the fork, when these forces are back in play, ICT must still be both inconsistent and incorrect.

This first Ellsworth failure is in not understanding the significance of the rear wheel for bicycles, particularly the “Center of Mass” issues discussed in the “Some Important Concepts” section.  This is most serious, since it leads to a false primary assertion of IC at the chain force line.  The following explains the fundamental physics that Ellsworth fails to understand.

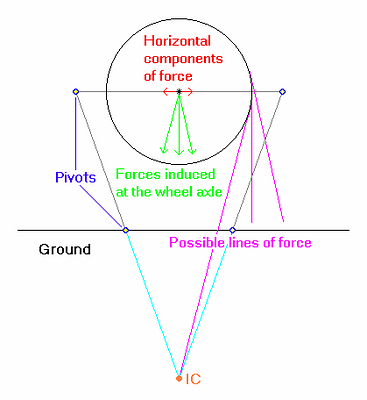
Recall again the pole and wheel experiment diagramed in Figure 2.5).  We can construct an analogous experiment for a 4-bar linkage.  Figure 5.4) shows a 4-bar rear suspension attached to the ground and balanced at equilibrium, with IC pictured.  For visual convenience only, we have mounted the axle at the mid point of the top link (rear link on a bike) in a symmetrical linkage.  This means that the tangent to the wheel path, at the point pictured, is horizontal.

Figure 5.4)

We put to Tony Ellsworth the question of where the rope should be pulled in the above contraption so that it does not fall.  Ellsworth replied that this was the first step in testing their ICT technology.  A cardboard and thumbtack model was constructed and experiments were done.  An experiment on a linkage porch swing was also cited as an example of the situation in Figure 5.4) (which, in their reply, they suggested I perform for myself).  Ellsworth concluded that the proper place to pull the chain in the above contraption is through the IC, if we wish the contraption not to fall.  By this time it should be obvious that the IC is not the direction to pull the chain.  As with the pole and wheel, one should again pull the chain (almost) vertically.

What Ellsworth has done is neglect the wheel!  This same error in the context of rear suspension is what causes inconsistency and incorrectness in ICT.

Mike Kojima also seems unaware of the considerations involved with the chain force being on the wheel.  In response to our statement in the “‘Pivot at the Chain Line' (PCL).” section that the pole and wheel from Figure 2.5) “should also have cast some serious doubt on this theory (again, think of the earth as a very large front triangle).” Kojima stated:

“His pole theory should make this more obvious!”

This seems to indicate that Kojima believes a rope pulled through the hinge would not cause the pole and wheel to fall.

Given Ellsworth's incorrect answer to the question and that Ellsworth considers this experiment equivalent to the linkage porch swing experiment, it is clear that Ellsworth does not grasp the significance of the wheel.  If the chain force in a bicycle were going directly into the rear link, instead of through the rear wheel, then the chain force line would be the place to put the IC, to at least make ICT theory consistent and correct, in the absence of acceleration and effects coming through the fork.  But since bicycles have wheels, ICT theory is inconsistent and incorrect, even in this case.