Figure 5.1).
Click to enlarge
Beware; this section is the most difficult in the work. An extremely strong physics background will be needed to tackle the last false theory in this section.
We have seen that Floating brake systems give a bike the breaking character of its linkage geometry. There is nothing special in this beyond what is noted in the “Braking.” section of Chapter III.
A number of theories out there claim advantages for floating brakes. But by this time, it should be trivial for the reader to prove most of these false.
For example, the idea that a floating brake will "isolate" braking from the suspension is as popular as the equivalent claim for 4-bar linkage suspensions [see BISL theory #2 of the “‘Brake Induced Shock Lockout' (BISL).” section]. This idea (also an “Internal Force” Theory) is also false for floating brakes for the same reason it is for 4-bar suspensions. As stated in other sections, “Nature Varies Smoothly” (NVS) and the “Coaxial Condition” establish that pivots do not “isolate” forces.
However, there is one very alluring theory for floating disc brakes, purporting striking increases in performance. We must examine this, as it has swayed even some very technically sophisticated people. Before we tackle it, though, we must cover a little background.
When two objects are in contact, there is a force called friction that opposes any sliding movement between the objects. Each object produces a frictional force that acts on the other.
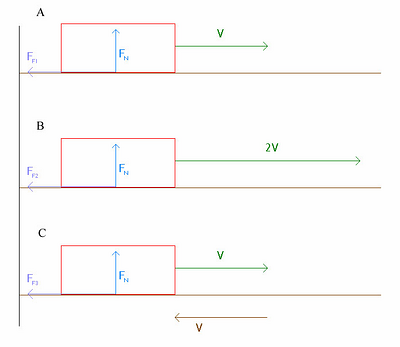
Consider, for example, Figure 5.1 A). Here is depicted a block sliding across a surface. The block has velocity V with respect to the lab, while the surface is stationary with respect to the lab. Depicted also is the normal force FN, acting from the surface to the block.
Figure 5.1).

Figure 5.1).
Click to enlarge
The frictional force between any two objects may be approximated with the following expression:
1) FF = c * FN,
where is c is the coefficient of friction. This approximation is often very good and in the case of disc brake pads on a disk rotor, probably exceptionally good.
!!! Note: The following is very important. It is the key to understanding why the theory below is not correct. FF does not depend on the relative velocity of the objects. It only depends on the normal force. !!!
There are two types of friction coefficients; one for static friction (when the objects are not moving with respect to one another) and one for kinetic friction (when the objects have relative motion). We will refer to the first as "c(s)" and the second as "c(k)". c(s) is generally much greater then c(k). The product of the appropriate coefficient of friction and the normal force between the two objects gives the magnitude of the frictional force acting on either object, which is directed opposite any propensity for movement of either object, relative to the other.
In Figure 5.1 A), we have labeled the frictional force "FF1" and we see that it is directed opposite the motion.
In a brake, the brake pads apply a normal force to the disc (rim), inducing a force of friction that may be described by equation 1).
Let us now examine the very alluring claim for floating disc brakes that we mentioned above:
Consider a bicycle rolling over rough ground. The normal force between the tire and ground is greater on the front side of a bump then it is on the rear of a bump. This means that a larger frictional, or braking, force may be applied between the tire and the ground on the front side of a bump, without losing static friction.
It is thought that brake rotation counter to the wheel up the front side of a bump and an opposite rotation forward down the back side of a bump will apply just such a variable braking force between the tire and the ground. Floating brakes rotate the rear brakes in just such a way (see Figure 3.12). But can the claim be true?
First, note that a bicycle rolling along the ground under braking may be modeled very well by a block sliding across a surface. Kinetic friction on the frame is just removed one step from the ground by the wheel. If we consider the wheel as part of the "ground" system, then we see that the "bike" system (which now does not include the wheels) looks very much like a sliding block, with (almost) all of the friction concentrated at the brake pads. (If the brake is not applied at the rim, then torque will come into play, but this is irrelevant to the questions at hand.)
So to understand the braking bike situation, let's look at the much less distracting, sliding block situation.
We have seen in Figure 5.1 A) that a force of friction FF1 acts to slow the block down. But the frictional force is not dependent on the velocity. Therefore, if the block were sliding across the surface with velocity 2V, as in Figure 5.1 B), the result would be frictional force FF2 = FF1.
Addition of velocities is linear in classical mechanics. We may thus switch reference frames and it is immediate that the situation in Figure 5.1 C), were the block slides with velocity V and the surface is now in motion with velocity -V, will produce frictional force FF3 = FF1 = FF2. It is also immediate that the acceleration of the block in all cases will be a1 = a2 = a3 = FF1/m, where m equals the mass of the block.
It is acceleration that we are interested in, after all, so we see that the rotation of the brakes back by floating brake systems is all for naught. This rotation back of the brake is analogous to the situation in Figure 5.1 C), which produces the same negative acceleration as the situation in Figure 5.1 A), which is analogous to a stationary brake.
Now floating brake proponents have countered with the following, involving the "energy" and "power" in the deceleration process.
2) Energy = Work = (Force)(Distance).
Also,
3) Power = (Energy)/(Time) = (Force)(Velocity).
All of the above quantities are average values over time.
It is noted that rotating the brakes backward increases the arc length of brake rotor that goes through the brake pads. This increases the energy value over a given time span and thus the power.
This increase in arc length is thought to be similar to increasing the radius at which the brake pads operate, which also increases the arc length.
Floating brakes are thus said to be more "powerful" then stationary brakes.
It is true that energy and power are increased when considering the relation between the brake pads and brake rotor. But this is irrelevant.
To see this, consider again our block sliding on a surface in Figure 5.1). The block decelerates the same in all cases. But the length of ground sliding under the block per time is greater in B) and C) then it is in A). This means that both the energy and power, as measured in the surface reference frame will be greater for B) and C) then it will be for A). But ultimately, it is the deceleration that we are concerned about. If the deceleration is not increased, then there is no advantage.
The above is a proof that Energy dissipated by a brake (the brake is the ground in this case) is irrelevant to the deceleration produced. But what is the problem fundamentally?
The problem, ultimately, is that energy is relative and not linear with velocity, and that those espousing floating brakes are only looking at one side of the process when reference frames are switched. The work done is increased, but so too is the relative energy. In the end, the two cancel out.
Put another way: The assertion is that there is something to be gained by the brake doing more work, while the bike/rider itself has no more kinetic energy with respect to the ground. But remember that the brake is moving with respect to the bike. This shift in reference frame will make the bike look like it has more kinetic energy, so nothing is gained.
An analogy may be drawn to our block sliding on the surface. If the block had a movable bottom that could be shifted back and forth relative to the main mass of the block, then the ground would "think" that the block had more kinetic energy while the bottom is shifted forward, in the direction of motion. But the deceleration would again be the same. (In fact, there would have to be "internal" energy released to shift the bottom forward, which is where the extra energy resides.)
As for increasing the radius at which the brake pads operate, that produces an increase in the lever arm and thus the torque. The increased braking force at the ground, for a given force to the brake lever, is due to this increase in torque and has nothing to do with the arc length of brake rotor traveling through the pads in a given amount of time.
Finally, one might think that the energy from compression of the suspension might be put into the brake and thus the bike would indeed have less energy compared to the work done by the brake, then in a fixed brake system. But this energy to compress the suspension ultimately comes from the kinetic energy of the bike. It is just transferred to the brake in a more roundabout way.
From an intuitive standpoint, consider whether or not your brakes stop you faster when you are traveling at a higher speed. If they did, brake modulation would be a very difficult thing.
It is really easy to do an experiment that will tell if the "Energy/Power" idea has any validity.
Construct a mechanism that will apply a constant amount of force too your rear brake lever; an elastic band should do fine. Then find out if it takes less time to slow from 30 mph to 25 mph then it does to slow from 10 mph to 5 mph.
In the first case, your brakes are doing far more work, but the deceleration will be the same.